What’s the best way to help your child nail third grade math? Food fractions! That slice of pizza is 1⁄8 of the pie. Compare 1⁄2 of a big doughnut with 1⁄2 of a small cookie — why aren’t they the same size? Instead of cutting that sandwich in half, experiment with thirds, fourths, and eighths. Talk through these food fractions with your child, and you’ll help your child understand this year’s most important math concept.
By the end of third grade math, here are the 10 key skills your child should learn (Four of them have to do with fractions!):
- Knowing the multiplication tables from 1 to 10 by heart.
- Multiplying and dividing with numbers up to 100.
- Understanding fractions as numbers that represent part of a whole.
- Placing fractions on a number line.
- Finding equivalent fractions.
- Comparing two fractions with the same numerator or denominator.
- Rounding numbers to the nearest 10 and 100.
- Telling time to the minute.
- Creating graphs to understand and solve word problems.
- Finding the perimeter and area of a rectangle.
Multiply, divide, and conquer math
Some things have to be committed to memory: name, address, date of birth — and the multiplication tables from 1 to 10. So much of math involves multiplication that your child needs instant recall of these products, from 1 x 1 = 1 to 10 x 10 = 100.
Beyond memorization, third graders need to understand multiplication as a way of finding the total number of objects without counting each one separately. Think of it as a quicker, more efficient way of adding.
For example: If Jessica has 4 boxes that are each stuffed with 7 teddy bears, how many teddy bears does she have? Jessica could dump them on the floor and count one by one, she could add 7 + 7 + 7 + 7, or she could multiply the number of boxes by the number of teddy bears in each box and quickly arrive at the answer, 4 x 7 = 28 teddy bears, in seconds. Being able to get that quick answer is nice, but it’s much more crucial that your child understand how and why all three methods work to get the same answer.
Just as your first grader learned to think of subtraction as the reverse or “undoing” of addition, your third grader needs to understand that division is like the reverse of multiplication. If multiplication is combining things, then division is breaking them apart into equal-sized groups. Math will make a lot more sense if your child understands the relationship between these two important operations.
For example: If 9 x 8 = 72, then 72 ÷ 8 = 9.
Third graders start learning the basics of algebra through multiplication and division by substituting an X for an unknown number and reversing the operation to solve for X.
For example: To solve 6 x X = 24, your child would divide 24 ÷ 6 = X. (And, if your child has memorized the multiplication tables, then she’ll know right away that X = 4.)
The two-step with word problems
Third graders now mainly solve two-step word problems that require using any of the four operations — addition, subtraction, multiplication, division — to solve.
For example: If 3 children pick 4 apples each, and then the group eats a total of 6, how many apples are left? Step 1: 3 children x 4 apples = 12 apples. Step 2: 12 apples – 6 apples = 6 apples left.
Rounding off
Third graders learn to round whole numbers up or down to the nearest tens or hundreds place.
For example: Round 62 to the nearest ten. (It’s 60.) Round 287 to the nearest hundred. (It’s 300.)
Your child will also add and subtract within 1,000 and learn the pattern for multiplying numbers by 10: adding a zero.
For example: If 6 x 6 = 36, then 6 x 60 = 360. See, not so intimidating now.
Fractions matter
These are the main things your child will learn about fractions in third grade.
- 1. Fractions are numbers and can be shown on a number line:
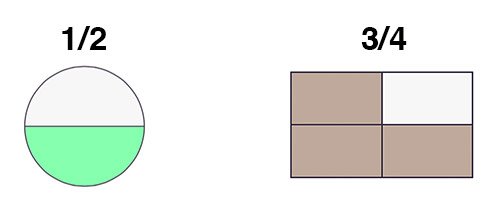
- 2. Fractions represent equal parts of a whole object or shape:
- 3. Whole numbers can be expressed as fractions: For example: 4 = 4⁄1 and 1 = 4⁄4
- 4. Fractions with different numerators (top number) and denominators (bottom number) can be equal:For example: 1⁄2 = 2⁄4 , 6⁄8 = 3⁄4

Time
Your third grader gets precise about the time, solving addition and subtraction word problems about time and telling time to the nearest minute.
For example: Jane’s alarm clock goes off at 7:00 a.m., but she doesn’t get out of bed until 8:25 a.m. How much longer did she sleep?
Graphs and measuring
Third graders learn to draw picture graphs and bar graphs to compare numbers in word problems that ask how many more or how many fewer objects there are in one category than in another.
Third graders measure the length of objects to the half and quarter inch and show the different lengths on a plot line.
Farm fresh eggs in a quadrilateral
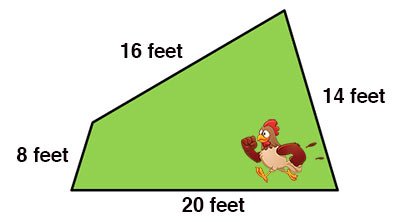
Third graders start using multiplication to find the area of a shape by multiplying length times the width. Kids expand their understanding of shapes based on shared properties. For example, not all four-sided shapes, called quadrilaterals, are squares and rectangles: some are kite shaped and some, like trapezoids, have four sides with different lengths. Your child will be asked to solve real-world problems to find the perimeter of these different shapes, too, by adding the lengths of all four sides.
For example: The chicken pen Gabriela’s dad is building needs a fence. The four sides measure 20 feet, 8 feet, 14 feet, and 16 feet. How much chicken wire does Gabriela’s dad need to buy?
Between food fractions — and maybe finding the area of a piece of bread now and then — you can do so much at home to reinforce the math skills your child needs to learn this year. Your child may not thank you for about 20 years, but eventually, your child will appreciate this crucial help.
Can your child multiply and divide like the third graders in our math Milestones video?





