¿Por qué son importantes las matemáticas de quinto grado? Es una pregunta que tu niño posiblemente te hará en algún momento este año. Así que esto es lo que hay que contestarle. Las matemáticas son la base de casi todos los descubrimientos científicos revolucionarios. Isaac Newton, parodiado en los dibujos animados por desarrollar la teoría de la gravedad después de que una manzana cayera sobre su cabeza, era un matemático.
A continuación te presentamos 8 habilidades matemáticas que tu hijo debería aprender para el final de quinto grado:
- Escribir ecuaciones y expresiones numéricas simples usando paréntesis ( ) y corchetes [ ].
- Trabajar con decimales y redondear decimales hasta las milésimas.
- Sumar y restar fracciones y números mixtos con denominadores diferentes (los números inferiores).
- Multiplicar y dividir fracciones.
- Dividir con divisores de dos dígitos.
- Convertir unidades de medida dentro del mismo sistema, entre ellos pies y pulgadas, kilómetros y metros.
- Interpretar datos y analizar relaciones, como velocidad y distancia, tablas, gráficas y diagramas de línea.
- Entender el volumen y encontrar el volumen de formas tridimensionales.
¡Qué patrón tan encantador!
Los problemas de matemáticas se vuelven un poco más sofisticados en quinto grado. En lugar de un simple 5 x 8 o 46 + 37, las ecuaciones tienen múltiples partes. Tu hijo comenzará a usar símbolos numéricos que le permitirán saber cómo resolverlos.
Por ejemplo: 3 x (51 + 97) indica que el 51 y el 97 deberían sumarse primero antes de multiplicarlos por 3.
Los estudiantes de quinto grado aprenden sobre los patrones dibujando gráficas y tablas que muestran la relación entre dos conjuntos de números que se relacionan.
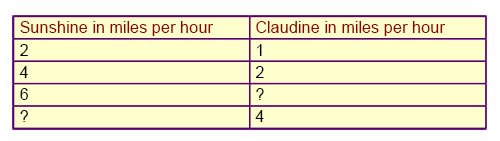
Por ejemplo: El perro de Claudine, Sunshine, corre dos veces más rápido que Claudine. Escribiendo correctamente el número faltante en la siguiente tabla, los estudiantes muestran que entienden el patrón en esta relación numérica.
Sunshine en millas por hora Claudine en millas por hora
La base 10
Los estudiantes de quinto grado trabajan mucho con decimales, que son una forma diferente de escribir fracciones donde el denominador siempre es 1, 10, 100 o 1.000. Los estudiantes ya entienden el valor posicional de los números enteros. Por ejemplo, en el número 429, el 9 está en el lugar de valor de las unidades, el 2 está en el lugar de las decenas y el 4 está en el lugar de las centenas. Del otro lado del punto decimal, el valor posicional disminuye una décima por cada valor que se mueve a la derecha. Por ejemplo, en el número 1,234, el 2 está en el lugar de las decenas, el 3 está en el lugar de las centenas y el 4 está en el lugar de las milésimas. Tu hijo aprenderá a leer y escribir decimales hasta las milésimas y a escribirlos como números, basándose en el 10 y en forma expandida.
Por ejemplo: 726,938 = (7 x 100) + (2 x 10) + (6 x 1) + [9 x ( 1⁄10)] + [3 x ( 1⁄100)] + [8 x ( 1⁄1000]
En forma expandida, 726,938 = setecientos veintiséis y novecientos treinta y ocho milésimas.
Tu hijo también aprenderá a sumar, restar, multiplicar y dividir decimales hasta las centésimas. Y cuando encuentre la respuesta, con frecuencia se le pedirá que redondee decimales hasta la decena, centena o milésima más cercana.
Por ejemplo: 0,487 se puede redondear hasta el lugar de las centenas; 0,49, o hasta el lugar de las decenas, 0,5.
Este año también se profundizará un poco más en la división. Los estudiantes de quinto grado dividirán números enteros de hasta cuatro dígitos entre números de dos dígitos y obtendrán números con residuos o respuestas con decimales.
Por ejemplo: 1.610 ÷ 80 = 20 R1 o 20,125.
Las fracciones pueden ser divertidas
En cuarto grado, tu hijo debería haber dominado cómo encontrar denominadores comunes (los números inferiores) en fracciones. Este año, los estudiantes de quinto grado utilizan esas habilidades para sumar y restar fracciones y números mixtos con denominadores diferentes.
Por ejemplo: 4 4⁄5 – 3 2⁄3 = 4 12⁄15 – 3 10⁄15 = 1 2⁄15.
También se espera que tu hijo resuelva problemas que contengan fracciones y números mixtos con denominadores diferentes.
Por ejemplo: Tenemos dos pasteles. Mary se come 5/8 de uno y Jack se come 1/3 del otro. ¿Cuánto pastel queda? Para responder a esto, tu estudiante de quinto grado tiene que encontrar el denominador común para ocho y tres, sumar las fracciones y a continuación restar lo que comieron del total para ver cuánto queda.
2 – ( 5⁄8 + 1⁄3) = 2 – ( 15⁄24 + 8⁄24) = 2 – 23⁄24 = 1 1⁄24 queda de pastel.
Los estudiantes de quinto grado aprenden a multiplicar dos fracciones, como, 1⁄2 x 1⁄2, y a multiplicar una fracción por un número entero, como 1⁄3 x 12. Los estudiantes necesitan aprender por qué al multiplicar un número entero mayor a 0 y una fracción menor a 1, el producto es siempre menor que el número entero.
Por ejemplo: 2 x 2⁄3 = 2⁄1 x 1⁄3 = 2⁄3 ( 2⁄3 es menor que 2).
Dando vuelta a las fracciones
También se les da vuelta a las fracciones este año mientras los estudiantes aprenden que dividir las fracciones y los números enteros no es lo que parece. Por ejemplo, dividir 8 entre 1⁄2 realmente es preguntar cuántas veces 1⁄2 cabe dentro de 8. La respuesta es 16. Por otra parte, dividir 1⁄2 entre 8 en realidad es preguntarse cómo dividir 1⁄2 entre 8 fracciones iguales y más pequeñas. La respuesta es 1⁄16.
Por ejemplo:
8 ÷ 1⁄2 = 8⁄1 ÷ 1⁄2 = 8⁄1 x 2⁄1 = 16
1⁄2 ÷ 8 = 1⁄2 ÷ 8⁄1 = 1⁄2 x 1⁄8 = 1⁄16
Medición por medición
La medición en quinto grado tiene que ver con aprender a convertir una unidad de medición a otra dentro del mismo sistema, y usar esas conversiones para resolver problemas de palabras.
Por ejemplo: Matthew pide 7 onzas de leche. Adriana pide una taza de leche. ¿Quién obtendrá más leche?
Por ejemplo: Jonathan puede correr un kilómetro en 11 minutos. Carol puede correr 3 metros por segundo. ¿Quién es más rápido?
Los estudiantes también tendrán que resolver estos problemas con fracciones y mostrarlos en un diagrama lineal.
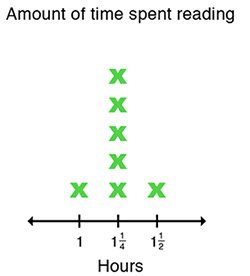
Por ejemplo: Marisa hace una encuesta entre sus compañeros de clase sobre cuántas horas pasan leyendo cada semana y muestra sus respuestas en un diagrama lineal.
Cantidad de tiempo que pasan leyendo
Suba el volumen
Los estudiantes de quinto grado mejoran su comprensión del volumen aprendiendo a medir el volumen de diferentes formas tridimensionales. Además de contar cuántas unidades de cubos se necesitan para llenar una forma, lo cual aprendieron en cuarto grado, los estudiantes aprenden a usar la fórmula para encontrar el volumen de un prisma rectangular V (volumen) = L (longitud) x W (ancho) x H (altura). Los estudiantes también aprenden la fórmula para encontrar el volumen de un prisma rectangular recto: V (volumen) = B (área de la base) x H.

Anima atru estudiante de quinto grado a que trabaje duro en matemáticas recordándole que las matemáticas nos ayudan a responder preguntas sobre los misterios del mundo, incluido cuánto caramelo de chocolate obtendrá si comparte esa 1/2 caja con tú y con su hermano, por supuesto.
Ve cómo les va a los estudiantes de quinto grado en nuestros videos de las Milestones matemáticas cuando tienen que enfrentarse a sumar y restar fracciones con denominadores diferentes.






