Your feedback is important to us
Please provide any feedback you have. Thank you!
Thank you!
Your feedback has been submitted.
 See if your state is part of the Smarter Balanced Assessment Consortium
See if your state is part of the Smarter Balanced Assessment Consortium
Please provide any feedback you have. Thank you!
Your feedback has been submitted.

See what skills are tested, understand your child's scores, and get ideas for how you can help at home.
Eighth graders should be able to recognize the techniques used to develop plots in fiction. For example, an author may create a crisis for characters to resolve together.
Students should also be able to compare a written version with a film version of a story or play. They should explain whether the film stays true to the text. To do this, they should be able to cite evidence and details from both versions.
In literature, eighth graders should be able to recognize how a character’s point of view can create suspense or humor. If one character is easily scared, for example, his reaction to the slightest noise may provoke a laugh.
Watch how a teacher gets middle schoolers to talk about what they’re reading.

Schedule a meeting with your child’s teacher to ask about her analytical reading skills. Can she analyze how authors use dialogue and events in a story? Does she select the best examples when summarizing fiction? Find out what you can do at home to help her analyze stories, plays, and poems.
When eighth graders summarize social studies or science texts they are expected to use evidence and leave out their own opinions on the topic. In an article about a species of zebra mussel invading the Great Lakes, for example, students should cite the damage described by the author in their summary about the species’ negative impact on the habitat. They should not add unsupported statements like The mussels are destroying the Great Lakes.
They should also be able to analyze how a science or social studies text is organized. In a text about the Egyptian pyramids, for example, a student could explain that the opening paragraph states the main idea of the entire section.
Watch how middle schoolers do research on a topic.

Eighth graders should be able to recognize when two texts on the same topic provide conflicting information. They should ask: What is different about the information each text provides? Which appears to be more reliable? Why?
Meet with your child’s teacher to find out how he’s doing. Can he select the best evidence when summarizing a text? Does he notice how texts are organized? Does he notice words that may be clues about author’s point of view? Find out how you can help your child become stronger in these analytical skills.
As they prepare for high school, eighth graders need to increase their knowledge of academic vocabulary (extensive and correlation) and figurative language (After she got angry, we were all walking on eggshells) and use a range of strategies to figure out new words.
By now they have read enough that they should be familiar with many references made through allusions (mention of historical and literary characters and events). It is hard, for example, to understand the sentence I was surprised his nose had not grown like Pinocchio’s if you have never read or heard the story of Pinocchio.
They should also be able to analyze the symbolism of analogies (a comparison of two things based on their structures or characteristics). For example, they should understand that a fish out of water is a reference to someone uncomfortable in their surroundings.
Eighth graders continue to learn about the connotation — or emotional association — of words and how it can provide clues about an author’s point of view.
For example, in the sentence A video showing a baby elephant painting a canvas resulted in the increased exploitation of the gentle animal, students should be able to point to the word exploitation as evidence that the author disagrees with training elephants to entertain tourists.
Negative or positive? — After reading an article together about a topic of his choice, ask your child to identify a few words that carry a negative or positive connotation. What does the use of these word tell us about the writer’s point of view?
A word a day — Build a bigger vocabulary, one word at a time. To help your child build his vocabulary, print out this list of words that eighth graders are expected to know. Try to use these words in conversation, and see if your child can use them correctly when talking with you. Listen for the words when watching a movie or a TV show. Challenge your child to find words he doesn’t know in articles on a website or in a magazine. This will help with your child’s reading, speaking, and writing this year — and these are also words your child needs to know for the SAT and ACT tests. Sign up for GreatWords, our free vocabulary-boosting text message program, to get daily text messages with 8th grade academic vocabulary words. To get started, text WORDS to 88769. (See terms and conditions.)
Ask your child’s teacher about his vocabulary knowledge. Find out what else you can do at home to help him build his word knowledge.
By eighth grade, students should be writing essays and stories that include strong organization, description, and evidence.
They should know which words are appropriate for which writing style. For example, they should use lots of sensory details when writing a story. In a report, however, they should include academic words specific to the topic. In all writing, students should use transition words and phrases (e.g., moreover and equally important) to make shifts between ideas, evidence, and events.
Eighth graders should also use techniques relevant to each writing style. They may include tables, graphs, or multimedia in their reports. When writing a story, they may use plot devices like flashbacks or foreshadowing to build the plot. In argument writing, eighth graders should be able to address opinions different from their own when building a persuasive argument.
Watch middle schoolers develop an informational essay.

Be free — If your child has trouble writing for assignments, the problems may be more emotional than intellectual. So help your child free up her mind before a dreaded writing assignment. The idea behind a free write is keep the pencil (or keyboard) moving for a specific amount of time and get past all those demons in your child’s head. Start with just three to five minutes. Tell her to write about anything or give her a prompt: What was the best single moment of your day? What would you like to do this weekend? As she gets comfortable with five minutes, try increasing the time to seven, then ten, etc.
Personal POV — It’s entirely normal for young teens to be focused on their own lives. Channel this energy by asking your child to write about a personal experience from his point of view (POV), like an argument with a sibling or why he loves or hates a certain sports team.
Read more! — That’s right; there’s a huge link between reading a lot and writing well. When your child reads things she likes, she absorbs new words and interesting turns of phrase that she can use in her own writing.
Ask your child’s teacher to show you some of your child’s writing and explain what she does well and what areas need improvement. Seeing an example will give you a better idea of areas where she needs help. Don’t forget to ask the teacher for ideas about activities to improve your child’s writing skills.
When eighth graders write, they need to know how to choose the appropriate mood for a specific tone they want to convey. For example, if they want to express wishfulness or desire, they might use the subjunctive mood (She hoped Emily would come to her party). If they want to set up the possibility that something could cause an action, they should use the conditional mood (The roof could collapse if you don’t get it fixed).
By now students should know that the active voice is clearer and easier to understand than the passive voice. John mailed the letter (active) is clearer than The letter was mailed by John (passive). However, to emphasize the uncertainty of who did something, passive voice is the better choice: The evidence was examined before the trial began.
As students’ writing becomes more sophisticated, they also learn more advanced punctuation techniques. They should know how to use an ellipsis (…), for example, to show when a thought has trailed off or to leave out unnecessary information. For example, After school I went to her house… and then came home.
Make it active — Write some sentences using the passive voice to analyze with your child. Ask her how you should rewrite the sentences to make them more active. Compare them and decide which sounds better.
Why punctuate? — After reading an article or story with your child, focus on how commas, dashes, and ellipses are used. Ask your child to explain how the marks add to the reader’s understanding of the text.
Meet with your child’s teacher to find out if your child needs help with grammar, punctuation, or spelling. What activities can you do at home to help your child improve these skills?

Functions describe relationships in which one thing is determined by another. For example, a teacher might say, Your grade in this class is a function of the effort you put into it. In math functions, when one number (known as the input or independent number) changes, that changes the next number (known as the output or dependent number). There is only one output for each input. Consider the following table. Your child may be asked whether or not it represents a function. The answer is no, because the number 1 appears two times with different outputs each time.

In eighth grade, students work with linear equations with two variables. Kids use functions to determine the proportional relationship between the two variables. This relationship is most commonly known as the slope.
A linear equation is written as y = mx + b. The m represents the slope and the b represents the y intercept, the point on the graph where the slope crosses the y-axis. It’s called a linear equation because when the outcomes are plotted on a graph, the points can be connected to form a line, like this graph that represents y = 2x +3. The y intercept is at (0,3).
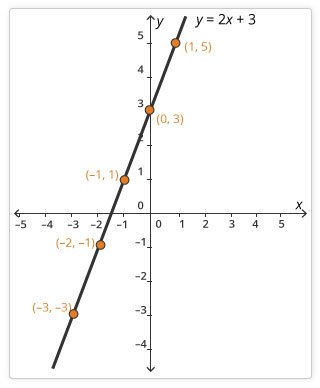
The study of functions leads to linear equations with two variables. These can be written several ways. The general form is ax + by = c. The slope intercept form is y = mx + b. Your eighth grader should know what each part of these equations represents.
A real-world example is when you want to compare the price of two gym memberships to see at what point one plan is cheaper than the other. For example, say Plan A charges a flat rate of $29/month with an initial fee of $99. The monthly fee of $29 is constant and will not change. This is the slope or rate of change of the line and is represented by the variable m. The variable b represents the y-intercept, which is the initial value or the fee of $99. Students learn that to figure out the cost of a gym membership for the year, start with $99 and add that to the $29 monthly times x months. This can be represented by the linear equation y = 29x + 99, where x is the number of months you’re a member and y is the total cost.
Students are expected to take a real-world situation like this, write a linear equation to represent it, and graph it.
Slope is used in geometry, too, as students learn how to apply the concept of slope in concrete terms using shapes, particularly triangles.
Remember the Pythagorean Theorem? The equation a2 + b2 = c2 is used to find the length of the hypotenuse, which is the side opposite the 90° angle in a right triangle. (Any triangle with a 90° angle is called a right triangle.) Here, the hypotenuse is the longest side of the triangle and it’s across from angle B, a right angle.
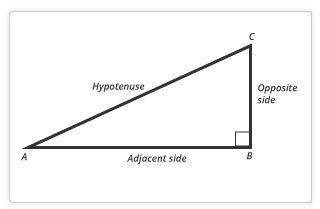
Want more? Watch this Khan Academy video for a demonstration of the Pythagorean Theorem.
Radical means “root.” Radical numbers are expressions that have a root sign, denoting square root, cube root, etc. (Square root, which looks like a check mark, √, is the most common radical.) The square root of a number is a smaller number that, when multiplied by itself, equals the original number. For example: the square root of 9 is 3 because 3 x 3 = 9.
Students will also work with exponents, which are like the opposite of roots. Exponents show how many times to multiply a number by itself. Exponents are written like this: 67 . Here, the 7, which seems to be sitting on the 6’s shoulder, is the exponent. The 6 is known as the base. Out loud, 67 is said 6 to the power of 7, and it means 6 times itself 7 times, or 6 x 6 x 6 x 6 x 6 x 6 x 6 = 279,936.
In eighth grade, students learn to work with negative exponents, such as 2-4. Negative exponents represent a fraction. Here’s an example of what your student might see:
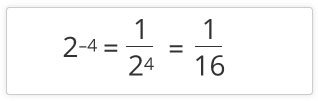
Is this really necessary? Yes. To be prepared for fractional exponents in high school algebra, your eighth grader needs to know how to rewrite expressions with positive and negative exponents now.
In functions, there is exactly one output (or answer) for every input. For example, in the function y = x – 2, for every value of x there is only one possible value of y.
Sample problem 1: Evaluating a function

Eighth graders start looking at two linear functions to determine where they will intersect with each other on a graph. This is called a system of linear equations.
Watch this video of eighth graders using linear equations to solve a real-world problem.

Sample problem 2: Solving a system of linear equations
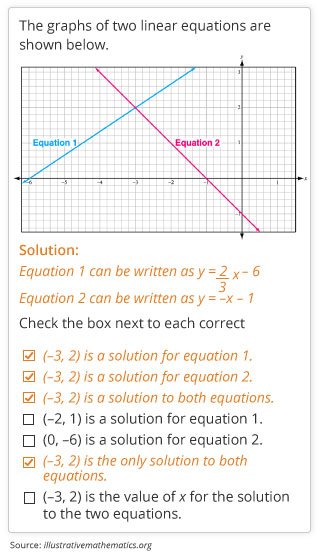
Watch an eighth grader solve a system of linear equations algebraically.

Eighth graders learn to solve equations that involve multiple steps and that have variables on both sides of the equal sign. For example:
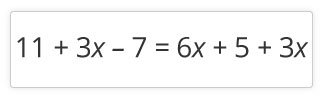
Equations with variables on both sides of the equal sign can have one answer, no answer, or infinitely many answers. Equations with no solution means that there is not a value that can be substituted for x that will make the sides equal. For example:
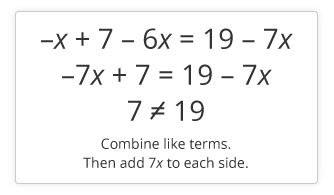
An equation with infinitely many solutions occurs when both sides of the equation are the same. For example:

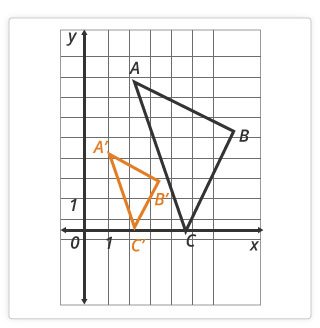
In eighth grade, students investigate what happens to a shape if it is flipped over (reflection), turned (rotation), or moved (translation). These are called transformations. Students also learn about enlarging shapes (dilation). Some questions eighth graders see involve multiple transformations to one shape. These are the transformations eighth graders learn about:
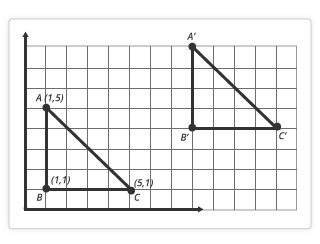
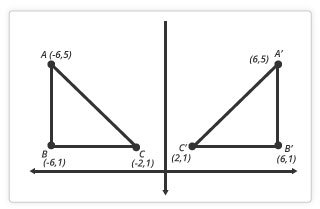
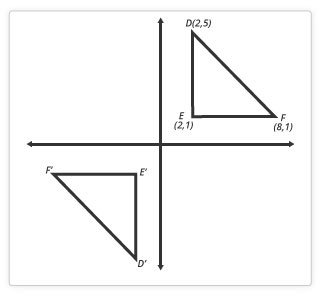
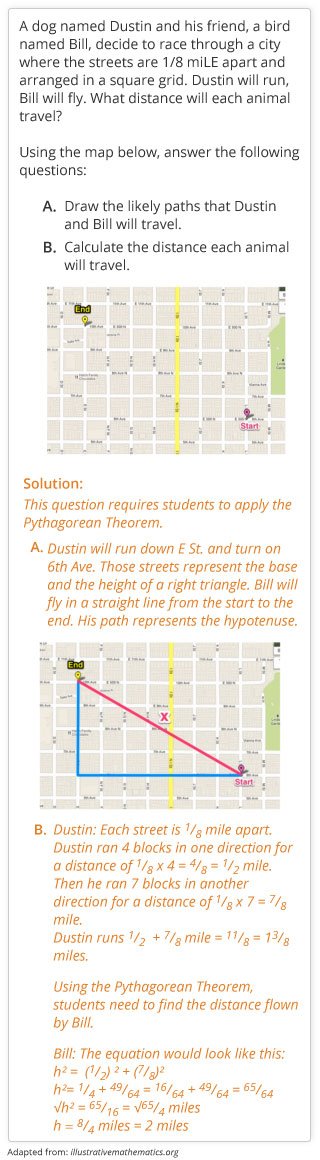
Eighth graders learn the equation for the Pythagorean Theorem, which is a2 + b2 = c2. It’s used to find the unknown length of a side of a right triangle when you know the lengths of the other two sides. (Tip: A right triangle has a 90o angle.) The Pythagorean Theorem is used in many everyday activities and jobs, from architecture to sports. Yes, sports. A baseball diamond is actually made up of two right triangles.
Sample problem 3: Applying the Pythagorean Theorem
Sample problem 4: Using exponents to find equivalent expressions

You know what they say: monkey see, monkey do. So, even if you’re one of the many people who suffer from math anxiety, it’s best for your child if you keep that dread under wraps. If you say things like I hate math, or worse, I just don’t have the math gene, your child will likely say these things, too. Research shows if you embrace math and show your child how useful it is in everyday life, your child’s attitude — and math scores — will be positively affected.
See how to model a growth mindset — and harness the power of yet — when talking to your child about math.

Even if you can’t (or just don’t want to) solve a linear equation, your child’s teacher will have ideas for how you can help at home. Tell the teacher about your child’s passions or extracurricular activities, such as baseball or drawing, and ask for suggestions for how to inject some eighth grade math into those pastimes.

If this were the Academy Awards, this category would be Best Supporting Actor and Actress. They’re not the stars, but the movie wouldn’t exist without them. This content is given less weight on the PARCC exam, but it supports the major work of the grade and sets your child up for success in future grades.
Now, let’s get radical and irrational — with numbers, that is.
Students learn to categorize numbers within the number system as rational or irrational. Remember: irrational numbers are numbers that cannot be expressed as a fraction; they are numbers that go on forever without any repeating numbers or sequences of numbers after the decimal. Pi — or π — is the most famous irrational number. Students usually write it as 3.14, but it actually keeps going on and on (and never ends).
Watch this video on rational and irrational numbers.
Eighth graders learn a new twist on the volume formula (v = l x w x h) they mastered in earlier grades. Why? They’ll be working with round objects, like spheres (v = 4/3 πr3) and cylinders (v = πr2h), where, for example, π is involved in finding the area of the base of the cylinder’s circle. They’ll also work with cones, which become thinner at one end (v = πr2 h⁄3).
Want to know the most important thing you can do to help your child with math? It’s having a positive attitude! Find ways to express and demonstrate your positive attitude about math. Why? Because research shows that a parent’s attitude toward math is contagious; so just by having a good attitude you are helping your child with math. So yes, you are a math whiz — and your child is one, too.
What is your child struggling with, exactly? For example, is it understanding the formulas? Or maybe it’s something in the application of a formula. Ask the teacher! When you find the glitch, you can help your child fix it together.

There’s a classic Monty Python sketch where a man goes into an argument clinic and finds that it’s not up to snuff. An argument isn’t just contradiction, he says to the professional arguer. Well! It CAN be! retorts the arguer. No it can’t! argues the customer. An argument is a connected series of statements intended to establish a proposition.
That’s the essence of Mathematical Reasoning. Students are expected to create arguments that support their work and share their reasoning. To do this, they’ll use what they know about numbers, equations, math rules, and models (charts, graphs, tables, etc.). Kids are expected to critique their classmates’ work and determine if an answer is correct or incorrect by identifying the strengths or the flaws in the math.
Sample problem 1: Critiquing solutions and explaining reasoning

Eighth graders need to be able to evaluate and defend their work and critique their classmates’ work. The goal is to help kids really understand whether problems are solved properly — and why. If there are errors, students have to identify what went wrong and figure out how to fix them.
Sample problem 2: Critiquing and correcting math reasoning

To paraphrase the noted astrophysicist Neil deGrasse Tyson: Kids don’t have an innate fear of full moons. They’ll play in a full moon with no worries at all. They only get scared of magic or werewolves from adults telling them scary stories. The same goes for math. The fear we express influences what our children think and believe. So don’t make math scary for your children and they’ll keep on computing without fear.
If you suspect your child might be struggling with math reasoning, make an appointment to speak with his teacher. Tell the teacher what you’ve noticed and ask, Is this a math issue or more about reading? What’s the best way to help my child build his math reasoning skills?

Eighth graders are expected to assess situations that could come up in everyday life and determine how to solve them. Modeling comes in handy in these situations. Modeling can mean a lot of things: diagrams, charts, tables, graphs, and even equations.
In eighth grade, students are expected to make sense of word problems that present situations they might encounter in the real world by using functions, expressions, equation, tables, graphs, and other representations. They’re also charged with understanding and applying the Pythagorean Theorem in the real world and to solve word problems.
When it comes to modeling and application, a required skill that sometimes goes unmentioned is the ability to identify which numbers, quantities, and relationships are important to finding the solution. In eighth grade and beyond, your child will increasingly encounter word problems with “extra” info in them — that is to say, data that would be present in a real-world situation but that wouldn’t be relevant to solving the problem. This ability to identify what’s important (and why) is a skill to work on with your child.
Problem solving requires students to choose which concepts and procedures to use and check their answers given the context of the problem. For example, in a right triangle, the hypotenuse is always the longest side. Does your child’s solution make sense given this math rule? It’s something your eighth grader should know and use to check her work.
As problem-solving skills develop, kids’ understanding of math concepts become more deeply ingrained.
A question from this section may be based on something a student could encounter in real life or a problem that does not have any context and is purely about math. Here is an example of a real-world problem.
Sample problem 1: Solving real-world problems

By now, eighth graders should understand how and why to use mathematical models. Students don’t learn concepts and procedures just to know them; they learn to be able to understand reality. Modeling is a key way to do that. In eighth grade, this concept gets driven home as students are expected to create and analyze increasingly complex models to make sense of real-world situations.
Sample problem 2: Modeling

The next time you or your child are muttering bad things about math, go outside, look at nature, and marvel at the amazing beauty of math — from flower petals to pine cones, spider webs to beehives, and the rotation of the planets and the moon.
People don’t go into teaching for the big bucks; they do it out of a desire to help others learn. Ask your child’s teacher where your child is struggling and what you can do to help out.

GreatKids created this guide to help you understand your child's state test scores and to support your child's learning all year long. We worked with SBAC and leading teachers in every grade to break down what your child needs to know and exactly how you can help